Il problema del bagnino è un problema di ottimizzazione, ideato dal fisico Richard Feynman, che prelude al principio di Fermat e alla legge di Snell.

---

Siamo al mare: un bagnino vede un bagnante in difficoltà.

Un uomo è in difficoltà nel punto N; il bagnino si trova in B. Che strada fa il bagnino per raggiungerlo?

Il bagnino corre sulla sabbia più rapidamente di quanto nuoti: quale percorso gli conviene seguire per arrivare dall’uomo il prima possibile?

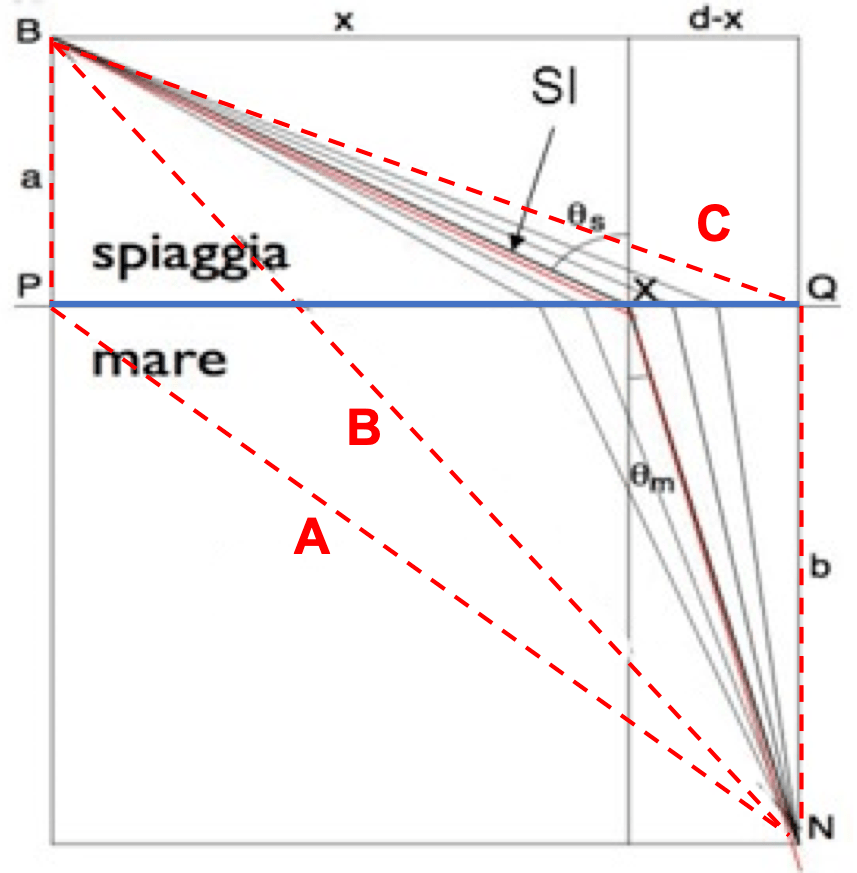
Il disegno schematizza la situazione:

• B è la posizione del bagnino; N quella del nuotatore;
• la linea blu indica la linea di separazione tra spiaggia e mare, con estremi in P e Q;
• disegniamo un rettangolo con vertici opposti in B ed N, con linee perpendicolari e parallele alla linea blu;
• chiamiamo a la distanza dal bagnino alla linea blu e b quella dalla linea blu al nuotatore;
• chiamiamo d la distanza orizzontale tra B ed N;
• se x è la distanza tra P ed il punto X in cui il bagnino entra in acqua, la distanza tra X e Q vale d – x.

Il bagnino andrà d’istinto ma un calcolo consente di trovare il punto X tale per cui la somma dei tempi da B a X, correndo sulla sabbia, più il tempo da X a N, nuotando, è il minimo possibile. Sul disegno sono tratteggiati in rosso tre percorsi alternativi:

• A: il bagnino entra in acqua nel punto più vicino, poi nuota;
• B: il bagnino segue una linea retta tra sé ed il nuotatore;
• C: il bagnino corre sulla spiaggia sino al punto più vicino al nuotatore, poi entra in acqua.

Abbiamo detto che il bagnino è più lento in acqua che sulla spiaggia; quindi, la traiettoria A è la più lenta; ma tra B e C? Facciamo un poco di calcoli.

• Chiamiamo v_T la velocità del bagnino sulla sabbia, e v_A quella in acqua;
• chiamiamo S_T lo spazio percorso dal bagnino sulla sabbia, e S_A lo spazio percorso in acqua;
• dal disegno si ricava: S_T = √(a² + x²); S_A = √(b² + (d – x)²)
• il tempo totale T vale: T = S_T/v_T + S_A/v_A

Del tempo T dovremmo calcolare il valore minimo. Questo si può fare con i metodi dell’analisi; per semplicità, è sufficiente tracciare il diagramma di come cambia T in funzione di X, e localizzare il minimo. Procediamo quindi dando alcuni valori di esempio.

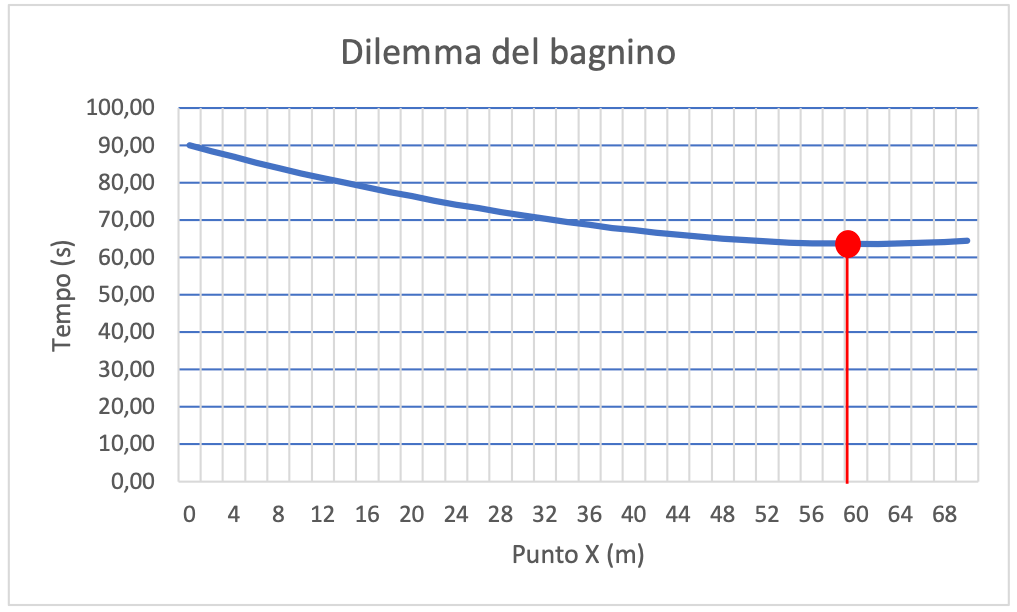
Supponiamo che sia: v_T = 5 m/s; v_A = 1 m/s (ottimo atleta!); a = 20 m; b = 50 m; d = 70 m (le proporzioni del disegno). Ora facciamo i calcoli, e disegniamo il diagramma. Come si vede, il tempo minimo si ottiene quando X si trova a 60 m: è il punto indicato nel disegno.

Bene, direte voi: è un problema interessante. Ebbene, è davvero un problema interessante, visto che lo ritroviamo in ottica, e persino in fisica quantistica! Come è possibile?

Rinviando la Fisica Quantistica ad un futuro remoto, anticipo i tempi, e accenno a come ritroviamo questo problema in ottica.

Voi tutti avrete osservato che, se guardate un oggetto parzialmente immerso nell’acqua, l’immagine della parte immersa è storta rispetto alla parte esterna. La spiegazione del fenomeno, che approfondiremo in futuro, è che la luce si propaga ad una velocità che dipende dal mezzo: più veloce nell’aria, più lenta nell’acqua. Supponiamo che A sia un punto esterno all’acqua, e B un punto nell’acqua. Domanda: quale traiettoria seguirà la luce per andare da A a B?

Il fenomeno fu studiato dal grande matematico e fisico Pierre de Fermat, che enunciò il seguente principio:

Il cammino percorso da un raggio di luce tra due punti è quello per cui il tempo impiegato dalla luce ad andare da un punto all’altro è minimo.

Vedete? È la stessa situazione del bagnino: anche la luce segue la traiettoria che minimizza il tempo totale! Ebbene, date le due velocità della luce, nell’aria e nell’acqua, si può calcolare la traiettoria della luce usando la stessa formula del bagnino!