Le equazioni di Eulero-Lagrange meritano un approfondimento dal momento che hanno aperto nuovi percorsi per la Fisica.
La parte di Fisica che abbiamo studiato in questi 38 articoli copre in maniera quasi completa il capitolo della fisica che si chiama Meccanica. Come avete visto, tranne quando abbiamo parlato di unità di misura e (il minimo necessario) di Matematica, tutti gli altri articoli (li potete trovare qui) hanno preso spunto da situazioni della vita quotidiana, che, spero, potete aver osservato, magari chiedendovi il perché del comportamento del fenomeno.
Citando lo scienziato inglese John Aldane, ci sono quattro stadi di evoluzione della conoscenza scientifica: anzitutto è una cosa assurda, poi è interessante ma perversa, poi vera ma irrilevante; infine: “Lo ho sempre detto”.
Nel nostro percorso abbiamo incontrato i personaggi principali che hanno contribuito allo sviluppo della materia. Citare gli scienziati serve a ricordare che la Fisica (e la Matematica) non sono scienze discese dal cielo: i loro principi non si trovano in nessun libro “ispirato”. Però, oggi, e specialmente oggi, è evidente che senza la Scienza la vita odierna sulla Terra sarebbe semplicemente impossibile.
Lo sviluppo della scienza si basa su uno stimolo, la curiosità di sapere, e su un approccio: l’onestà nel riconoscere che i fatti superano tutte le opinioni e teorie. Questo è il motivo per cui, conscio dei miei limiti, ho cercato di rispondere alle vostre curiosità. Mentre vi parlavo ho spesso osservato una evoluzione del vostro atteggiamento su ciò che vi raccontavo. All’inizio: “Mai visto, chissà di cosa parla”; poi: “È vero, non ci avevo mai pensato”; infine: “Incredibile, è proprio vero: è così che succede! Ma allora, se…”
La parte più importante è l’ultima: presa conoscenza dei fatti e delle spiegazioni che vi porto, iniziare ad allargare quanto avete sentito ad altre situazioni, che avete osservato senza poterle spiegare.
Bene: dai prossimi articoli cambieremo argomento; ci chiederemo anzitutto come è fatta la materia, e poi vedremo i fenomeni della termodinamica: il motivo per cui funzionano i motori delle nostre auto.
Concludendo su quanto abbiamo imparato della Meccanica, abbiamo: le tre leggi di Newton, poi la legge sull’impulso e la quantità di moto, poi le definizioni di energia cinetica e potenziale, poi la costanza dell’energia in un sistema isolato.
Quante leggi sparse! Non c’è, per caso, una legge che unifichi tutto quanto?

Ebbene, c’è! La formulazione di questa legge è merito di due geni: Eulero (Leonhard Euler), e Giuseppe (Joseph – Louis) Lagrange.
La spiegazione del loro lavoro è materia di università, ed è alquanto intricata perché richiede delle ulteriori conoscenze di Matematica: mi dispiacerebbe, però, concludere il nostro discorso senza nemmeno accennarvelo.
Leonhrad Euler è nato a Basilea il 15/4/1707. Nella sua vita si è spostato in diversi paesi europei: a San Pietroburgo, dal 1726, poi a Berlino, nel 1741, ed infine ancora a San Pietroburgo, nel 1766, dove rimase sino alla morte, il 18/9/1783. Come si conveniva a quell’epoca per i grandi scienziati, il suo nome fu latinizzato in Eulero. È impossibile persino fare una breve sintesi del suo lavoro: Eulero è uno dei (cinque?) più grandi matematici di tutti i tempi. Cito solo la celebre formula eiπ+1 = 0, sintesi degli studi sui numeri complessi, battezzata “la formula di Dio”. La formula che ci interessa è stata sviluppata nell’ambito dello studio delle equazioni differenziali.

Giuseppe Lagrange è nato a Torino il 25/1/1736; nel 1766 fu chiamato a Berlino per sostituire Eulero (!) all’accademia di Berlino; nel 1787 si trasferì a Parigi, dove visse sino alla morte, il 10/4/1813. Malgrado la nascita e la giovinezza in Italia, tutti lo considerano francese: in effetti, era europeo. Il suo capolavoro è stato la Mécanique analytique, del 1788, dove getta le basi della meccanica razionale.
Riporto qui la definizione di “meccanica razionale” data da Wikipedia:
Branca della Fisica che studia il moto e l’equilibrio dei sistemi meccanici con un numero finito di gradi di libertà.
Subito un esempio: il pendolo.
Ricordate? Ne abbiamo parlato diverse volte: la cosa più importante, scoperta da Galileo, è che il pendolo percorre archi piccoli (meno di 5°) in tempi uguali (legge dell’isocronismo delle piccole oscillazioni del pendolo). Questa scoperta è stata fondamentale per costruire gli orologi a pendolo. Ebbene: da dove arriva? Come si dimostra?
Ebbene, l’equazione di Lagrange (nota anche come equazione di Eulero – Lagrange), consente di trovare la soluzione al problema: infatti, il pendolo è un sistema con un vincolo, il perno attorno a cui oscilla; quindi, ha un solo grado di libertà. Chi vuole seguirmi per vedere (meglio, intravvedere) come funziona? Attenti: da qui in poi procedete a vostro rischio e pericolo!
Cominciamo con due premesse. La prima, semplicissima: se cercate su Internet l’espressione della lagrangiana, troverete, tra le variabili, q̇ (oppure q’): la q con un puntino sopra (o con un accento). Di cosa si tratta?
Anzitutto, non spaventatevi, q è semplicemente una variabile dipendente dal tempo t, come x, y, z, θ. E il puntino sopra? Anche questo è semplice: è un altro modo di scrivere la derivata prima della variabile rispetto al tempo: quindi, q̇ = dq/dt: è una velocità, e si legge “qu punto” oppure “qu primo”. E per l’accelerazione, cioè per la derivata seconda? Due puntini! Per inciso, questa era il modo usato da Newton per scrivere le derivate; lui le chiamava flussioni.
Seconda premessa: sempre nella lagrangiana, trovate qualcosa come δL/δq. Che roba è questa?
Considerate una carta geografica: le montagne sono indicate con delle curve di livello, giusto? Ebbene, dal punto di vista matematico un punto sulla montagna è individuato da tre coordinate: x, y, z, dove x e y sono le coordinate della base, e z è l’altezza; quindi, z(x, y) dipende dalle due coordinate della base, e non da una sola. E se volete conoscere la pendenza della montagna lungo la direzione x? Semplice: si tratta di calcolare la derivata di z rispetto a x, ignorando la y. Quindi, invece di scrivere dz/dx, scriviamo δz/δx: si chiama “derivata parziale di z rispetto a x”. Chiaro? Semplice?
Ebbene, si chiama equazione lagrangiana L l’espressione:
L = K – U
Voi direte: che strano! Abbiamo imparato che K + U è l’energia totale di un corpo, ed è costante in un sistema isolato; c’è un errore? No, nessun errore: è proprio così! E quindi, cosa facciamo con questa equazione lagrangiana così definita? Ecco l’equazione di Eulero – Lagrange!
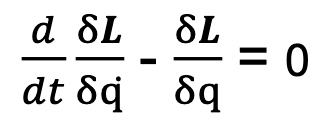
Leggiamola: la derivata rispetto al tempo della derivata parziale della lagrangiana rispetto a q̇ meno la derivata parziale della lagrangiana rispetto a q è uguale a zero.
Il fatto è che, con una scelta opportuna della variabile, con questa equazione si può studiare il comportamento dinamico di un qualunque sistema di corpi con vincoli, molle, carrucole e tutto quello che volete. Ho evidenziato il fatto che la scelta della variabile è molto importante per evitare di cadere in espressioni complicate.
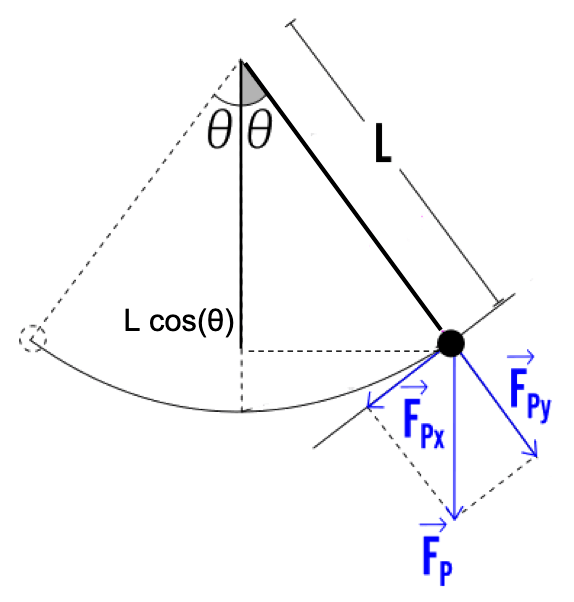
Armati di questo bagaglio, andiamo avanti con il pendolo. Consideriamo la massa del nostro pendolo: oscilla attorno al suo perno in cima all’asta. Ad ogni momento, la massa ha una certa energia cinetica, dovuta al fatto che si muove, ed una certa energia potenziale, perché si trova sopra al suo punto più basso.
La massa si muove per l’azione della forza peso, Fp = mg; la forza si scompone (regola del parallelogramma!) secondo due direzioni: quella dell’asta, che è annullata dal perno di supporto, e quella tangente all’arco di cerchio percorso dalla massa, che la fa oscillare.
Per definire l’energia cinetica della massa, prendiamo come variabile l’angolo θ dell’asta rispetto alla verticale. Ricorderete che, usando i radianti, la lunghezza dell’arco è il prodotto dell’angolo per il raggio; nel nostro caso, Lθ. La velocità v di rotazione della massa rispetto al perno è
v = dLθ/dt = Ldθ/dt = Lθ̇’
Quindi, l’energia cinetica è K = ½ m v2 =½ m L2θ’2.
Calcoliamo ora l’energia potenziale della massa del pendolo: di quanto può cadere? Al massimo, l’altezza della caduta è
L – Lcos(θ) = L(1-cos(θ)).
Quindi, l’energia potenziale è:
U = mgh = mgL(1-cos(θ)).
Allora: applichiamo l’equazione di Eulero – Lagrange al pendolo: riusciamo a trovare come si muove? Considerando che q = θ, cioè l’angolo che abbiamo scelto come variabile, e che θ’ è la derivata dell’angolo rispetto al tempo, e cioè la velocità angolare, abbiamo:
L = K – U = ½ m L2θ̇’2 – mgL(1-cos(θ)) = ½Lθ̇’2 – g + gcos(θ)
Primo passo: calcoliamo
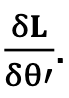
Poiché θ̇’ non è una variabile di U, abbiamo:
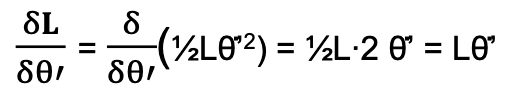
Secondo passo: calcoliamo:
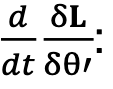
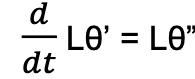
; questo perché l’unica variabile funzione del tempo è la derivata dell’angolo θ’, cioè la velocità angolare: la sua derivata, θ̇”, è l’accelerazione angolare.
Terzo passo: calcoliamo
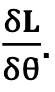
Poiché θ non appare nell’energia cinetica K, abbiamo:
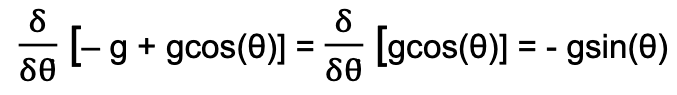
Quindi abbiamo:

Da cui:
Lθ” + gsin(θ) = 0
E infine:
θ” = -(g/L)sin(θ)
Questa è una equazione differenziale del secondo grado, perché θ” è l’accelerazione angolare. E come si risolve una equazione differenziale del secondo grado?
Procedendo per la via diretta, occorrono mesi di studio dell’analisi matematica. Prendendo una scorciatoia, ricordiamo che
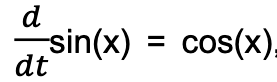
e che
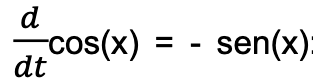
quindi, il movimento del pendolo è una sinusoide (lo si chiama moto armonico)! E con che periodo? Vi chiedo un ultimo atto di fede: dall’equazione differenziale si ricava che il periodo T è:
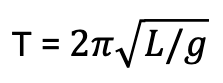
E ora sono contento di avervi così assillato? Si, perché l’importanza della lagrangiana va oltre alla meccanica classica. Oggi la Fisica Quantistica si basa su una serie di equazioni, una per ogni particella: ebbene, sono equazioni lagrangiane!

