La teoria cinetica dei gas spiega il comportamento dei gas in base alle loro particelle costituenti. Afferma che i gas sono composti da particelle in continuo movimento casuale, con energia cinetica proporzionale alla temperatura assoluta, e che le collisioni tra di esse sono elastiche.

---

Allora, riprendiamo il discorso: abbiamo tre leggi separate dei gas; possiamo ricavarne una sola? Vi ho già risposto di sì, ed effettivamente, partendo dalle tre leggi ed aggiungendo qualcosa, si può arrivare alla formula unificatrice.

Però io preferisco seguire un’altra strada: preferisco ritornare alla descrizione della materia che vi ho fatto, cioè di un insieme di atomi o molecole, e ottenere la formula che cerchiamo, ed altro ancora, partendo da questa descrizione. Prima di cominciare, una bellissima immagine di maggio 2021: quello che vedete sono gli atomi di un cristallo, Ortoscandato di praesodimio (PrScO₃), che oscillano attorno alla loro posizione. Vedere gli atomi è un risultato epocale!

Per illustrarvi questa strada utilizzo nientemeno che il libro “Lezioni di Feynman sulla fisica”, che spiega tutta la fisica agli studenti universitari. Non vi spaventate: Feynman è un mago nello spiegare con parole semplici. Quella che affrontiamo si chiama Teoria cinetica dei gas.

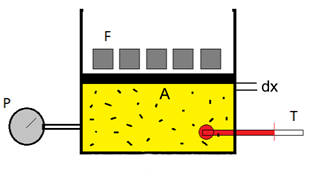
Allora, cominciamo con il nostro cilindro, che ha all’interno del gas. Noi possiamo misurare pressione P, temperatura T e volume V del gas, che è composto di numerosissimi atomi.

Prima ipotesi semplificativa: diciamo che si tratta di un gas monoatomico, come l’elio. Il problema con gas diversi è che quando gli atomi si scontrano possono subentrare urti anelastici: con l’elio, ed i gas nobili, questo fenomeno è remoto.

Seconda ipotesi semplificativa: il pistone scorre senza attrito. In questa situazione, la pressione P nel gas è data dal rapporto tra la forza F applicata al pistone e l’area A del pistone stesso: P = F/A.

Ora, cominciamo a comprimere il pistone, aumentando la forza F. Supponiamo che la variazione di forza sia infinitesimale: il pistone si sposterà di una quantità infinitesimale, che abbiamo indicato con dx.

La forza moltiplicata per lo spostamento è un lavoro: quindi, per spostare il pistone di dx, abbiamo fatto un lavoro infinitesimale, dW, che vale: dW = – F∙dx. Ma poiché F = P∙A, abbiamo:

dW = – P∙A∙dx = – P∙dV

Note: il lavoro è negativo perché siamo noi che schiacciamo il pistone; inoltre, dV = A∙dx: lo spostamento dx causa la variazione dV del volume.

Bene: noi applichiamo la forza F al pistone; dall’altra parte del pistone, che cosa la contrasta? Provate ad immaginarvi: all’interno del pistone c’è un numero enorme di atomi di elio che si muovono di continuo. Quindi, diciamo ad ogni secondo, un notevole numero di atomi collideranno tra di loro, ed anche contro le pareti del contenitore; in particolare, contro il cilindro. Cosa succede durante questi urti?

Come dicevo prima, gli atomi di elio si comportano come oggetti materiali puntiformi, che, durante gli urti, sono perfettamente elastici: per loro valgono le leggi, che abbiamo studiato, della costanza della quantità di moto e della costanza dell’energia del sistema. Voglio dire che, per spiegare le strane leggi dei gas, ci rifacciamo alle semplici leggi della meccanica newtoniana!

Ma voi mi chiedete: ma sono valide queste ipotesi? Non è che i risultati che otterremo saranno in totale contrasto con le leggi dei gas? Tranquilli: i risultati saranno in perfetto accordo con le leggi dei gas, purché temperature e volumi siano ragionevoli: per essere più precisi, purché il gas sia ben lontano dal liquefarsi. E perché questa limitazione? Perché, al limite della liquefazione, gli atomi dei gas tendono ad incollarsi: gli urti non sono più elastici! E come stiamo con l’elio? Benissimo: l’elio liquefa a soli 5 K circa; non c’è da preoccuparsi.

Allora, riprendiamo il discorso: la conclusione è che la pressione esercitata sullo stantuffo è equilibrata dagli urti elastici degli atomi di elio contro il pistone. Riuscite a immaginarlo?

Allora: se ogni atomo ha massa m e velocità v, cosa può succedere quando è vicino al pistone? Chiamando x la direzione ortogonale al pistone, può succedere che la componente v_x della velocità sia diversa da zero, e che l’atomo colpisca il pistone con un urto p_x di valore p_x = m∙v_x, dove m è la massa dell’atomo di elio. Attenti, però: poiché l’urto è elastico, il pistone respinge l’atomo con lo stesso impulso; in totale, il pistone è sottoposto ad un impulso:

2∙p_x = 2∙m∙v_x.

Ciò detto, nell’intervallo di tempo t, quanti atomi colpiranno il pistone? Chiaramente, se un atomo è lontano e t è piccolo, non colpirà il pistone; la distanza massima perché avvenga l’urto è v_x∙t! E poiché A è la superficie del pistone, gli atomi che lo colpiscono occupano il volume v_x∙t∙A! Chiaro?

Altro passetto avanti: supponiamo che N sia il numero di atomi contenuti nel cilindro: la densità degli atomi è n = N / V. Ma allora, il numero di impulsi ricevuti dal pistone nel tempo t vale n∙v_x∙t∙A; il numero d’impulsi al secondo vale: n∙v_x∙A. Concludendo, ad ogni secondo, il pistone è sottoposto ad una forza (ricordate: Ft = mv; abbiamo scelto il tempo di 1 s) che è il prodotto del numero di atomi per l’impulso esercitato da ogni atomo:

F = n∙v_x∙A∙2∙m∙v_x

Ma allora, la pressione esercitata dagli atomi di gas che urtano il pistone è:

P = F / A = 2∙n∙m∙v_x²

Beh, forse stiamo correndo troppo, e dobbiamo riflettere sulla velocità v_x. Difatti, non è ragionevole pensare che tutti gli atomi abbiano la stessa velocità v: in realtà, le velocità variano moltissimo da un atomo all’altro. E allora?

Allora dobbiamo considerare la velocità media <v_x>; meglio, la media dei quadrati, <v_x²>; quindi, riscriviamo:

P = n∙m∙<v_x²>

Ehi: è spirito il fattore 2! Perché? Perché, nel fare la media, troviamo che metà degli atomi hanno la componente v_x diretta verso il pistone, e metà in senso opposto!

Ehi, ehi: ma la componente v_x non è per niente speciale rispetto alle componenti ortogonali, v_y e v_z! E allora? E allora, in media, la media quadratica della componente <v_x²> sarà un terzo della media quadratica di v: <v_x²> = <v²>/3. A questo modo la direzione x non ha più nulla di speciale. Quindi, possiamo riscrivere la pressione come segue:

P = ⅓∙ n∙m∙<v²>

Oppure a questo modo:

P = (2/3)∙n∙<mv²/2>

Nell’ultima scrittura abbiamo evidenziato <mv²/2>, che è l’energia cinetica media degli atomi. Ora, finalmente, ricordando la definizione di n, possiamo scrivere:

P = (2/3)∙(N/V)∙<mv²/2>

Ovvero:

P∙V = (2/3)∙N∙<mv²/2>

Guardiamoci indietro per un momento, e vediamo il cammino percorso. Partendo dalla ipotesi che il gas sia fatto di atomi liberi, con semplici passaggi, siamo arrivati ad una formula che ci è familiare. Ricordate la legge di Boyle, per cui, a temperatura costante, il prodotto P∙V è costante? Ma è quello che abbiamo appena finito di scrivere! Però, diversamente dalla legge di Boyle, abbiamo scoperto in cosa consiste questa costante: a parte il coefficiente numerico 2/3, è il prodotto del numero N di atomi presenti nel gas per l’energia cinetica media degli atomi!

Cosa ci manca per arrivare ad una legge universale dei gas, che includa P, V e T? Ci manca valutare il numero di atomi N presenti nel gas, e l’energia cinetica media degli atomi, cioè <mv²/2>.

Ebbene, il traguardo è vicino!

---